Часто утверждают, что проектирование нейронных сетей, использующих алгоритм обратного распространения ошибки, является скорее искусством, чем наукой. При этом имеют в виду тот факт, что многочисленные параметры этого процесса определяются только на основе личного практического опыта разработчика. В этом утверждении есть доля правды. Тем не менее, приведем некоторые общие методы, улучшающие производительность алгоритма обратного распространения ошибки.
1. Режим обучения
Существует два режима обучения: последовательный и пакетный. В процессе обучения многослойного персептрона с применением алгоритма обратного распространения ошибки ему многократно предъявляется предопределенное множество обучающих примеров. Один полный цикл предъявления полного набора примеров обучения называют эпохой. В последовательном режиме корректировка весов проводится после подачи каждого примера. Это наиболее часто используемый режим. В пакетном режиме обучения корректировка весов проводится после подачи в сеть всех обучающих примеров одной эпохи. Последовательный режим обучения в вычислительном смысле оказывается значительно быстрее. Это особенно сказывается тогда, когда обучающее множество является большим и в высокой степени избыточным.
2. Максимизация информативности
Как правило, каждый обучающий пример, предоставляемый алгоритму обратного распространения ошибки, нужно выбирать из соображений наибольшей информационной насыщенности в области решаемой задачи. Для этого существуют два общих метода:
- использование примеров, вызывающих наибольшие ошибки обучения;
- использование примеров, которые радикально отличаются от ранее использованных.
Эти два эвристических правила мотивированы желанием максимально расширить область поиска в пространстве весов.
В задачах классификации, основанных на последовательном обучении нейронной сети алгоритмом обратного распространения ошибки, обычно применяется метод случайного изменения порядка следования примеров, подаваемых на вход многослойного персептрона, от одной эпохи к другой. В идеале такая рандомизация приводит к тому, что успешно обрабатываемые примеры будут принадлежать к различным классам.
Более утонченным приемом является схема акцентирования, согласно которой более сложные примеры подаются в систему чаще, чем более легкие. Простота или сложность отдельных примеров выявляется с помощью анализа динамики ошибок (в разрезе итераций), генерируемых системой при обработке обучающих примеров. Однако использование схемы акцентирования приводит к двум проблемам, которые следует учесть:
- распределение примеров в эпохе, представляемой сети, искажается;
- наличие исключений или немаркированных примеров может привести к катастрофическим последствиям с точки зрения эффективности алгоритма. Обучение на таких исключениях подвергает риску способность сети к обобщению в наиболее правдоподобных областях пространства входных сигналов.
3. Функция активации
Многослойный персептрон, обучаемый по алгоритму обратного распространения ошибки, может в принципе обучаться быстрее, если сигмоидальная функция активации нейронов сети является антисимметричной, а не симметричной. Функция активации называется антисимметричной, если:
Стандартная логистическая функция не удовлетворяет этому условию. Эта функция асимметричная:
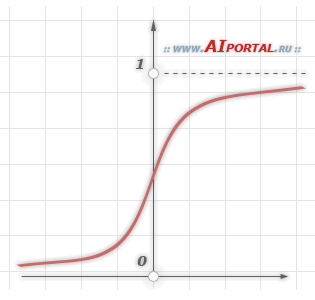
А эта антисиметричная:
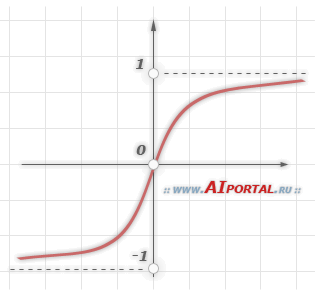
4. Целевые значения
Очень важно, чтобы целевые значения выбирались из области значений сигмоидальной функции активации. Более точно, желаемый отклик нейрона выходного слоя многослойного персептрона должен быть смещен на некоторую величину от границы области значений функции активации в сторону ее внутренней части. В противном случае алгоритм обратного распространения ошибки будет модифицировать свободные параметры сети, устремляя их в бесконечность, замедляя, таким образом, процесс обучения и доводя скрытые нейроны до предела насыщения.
5. Нормализация входов
Все входные переменные должны быть предварительно обработаны так, чтобы среднее значение по всему обучающему множеству было близко к нулю, иначе их будет сложно сравнивать со стандартным отклонением. Для оценки практической значимости этого правила рассмотрим экстремальный случай, когда все входные переменные положительны. В этом случае синаптические веса нейрона первого скрытого слоя могут либо одновременно увеличиваться, либо одновременно уменьшаться. Следовательно, вектор весов этого нейрона будет менять направление, что приведет к зигзагообразному движению по поверхности ошибки. Такая ситуация обычно замедляет процесс обучения и, таким образом, неприемлема. Чтобы ускорить процесс обучения методом обратного распространения, входные векторы необходимо нормализовать в двух следующих аспектах:
- входные переменные, содержащиеся в обучающем множестве, должны быть некоррелированы (см. математический анализ);
- некоррелированные входные переменные должны быть масштабированы так, чтобы их ковариация была приближенно равной. Тогда различные синаптические веса сети будут обучаться приблизительно с одной скоростью.
На рисунке показан результат трех шагов нормализации: смещения среднего, декорреляции и выравнивания ковариации, примененных в указанном порядке.
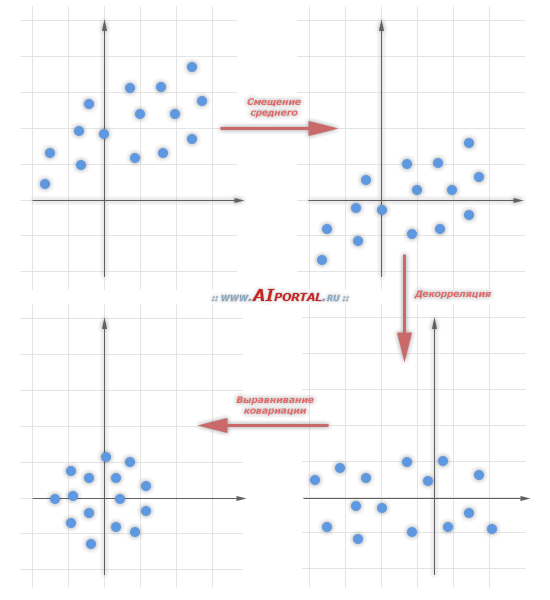
6. Инициализация
Хороший выбор начальных значений синаптических весов и пороговых значений сети может оказать неоценимую помощь в проектировании. Но какой выбор является хорошим? Если синаптические веса принимают большие начальные значения, то нейроны, скорее всего, достигнут режима насыщения. Если такое случится, то локальные градиенты алгоритма обратного распространения будут принимать малые значения, что, в свою очередь, вызовет торможение процесса обучения. Если же синаптическим весам присвоить малые начальные значения, алгоритм будет очень вяло работать в окрестности начала координат. В частности, это верно для случая антисимметричной функции активации, такой как гиперболический тангенс. К сожалению, начало координат является стационарной точкой, где образующие поверхности ошибок вдоль одной оси имеют положительный градиент, а вдоль другой – отрицательный. По этим причинам нет смысла использовать как слишком большие, так и слишком маленькие начальные значения синаптических весов. Как всегда, золотая середина находится между этими крайностями.
7. Обучение по подсказке
Обучение на множестве примеров связано с аппроксимацией неизвестной функцией отображения входного сигнала на выходной. В процессе обучения из примеров извлекается информация о функции и строится некоторая аппроксимация этой функциональной зависимости. Процесс обучения на примерах можно обобщить, добавив обучение по подсказке, которое реализуется путем предоставления некоторой априорной информации о функции. Такая информация может включать свойства инвариантности, симметрии и прочие знания о функции, которые можно использовать для ускорения поиска ее аппроксимации и, что более важно, для повышения качества конечной оценки.
8. Скорость обучения
Все нейроны многослойного персептрона в идеале должны обучаться с одинаковой скоростью. Однако последние слои обычно имеют более высокие значения локальных градиентов, чем начальные слои сети. Исходя из этого, параметру скорости обучения в алгоритме обратного распространения ошибки следует назначать меньшие значения для последних слоев сети и большие – для первых. Чтобы время обучения для всех нейронов сети было примерно одинаковым, нейроны с большим числом входов должны иметь меньшее значение параметра обучения, чем нейроны с малым количеством входов. Есть мнение, что целесообразно назначать параметр скорости обучения для каждого нейрона обратно пропорционально квадратному корню из суммы его синаптических связей.