Вывод в формальной логической системе является процедурой, которая из заданной группы выражений выводит отличное от заданных семантически правильное выражение. Эта процедура, представленная в определенной форме, и является правилом вывода. Если группа выражений, образующая посылку, является истинной, то должно гарантироваться, что применение правила вывода обеспечит получение истинного выражения в качестве заключения.
Наиболее часто используются два метода. Первый – метод правил вывода, или метод естественного (натурального) вывода, названный так потому, что используемый тип рассуждений в исчислении предикатов приближается к обычному человеческому рассуждению. Второй – метод резолюций. В его основе лежит исчисление резольвент.
В этой статье рассматривается метод правил вывода. В логике предикатов используется правило, которое из двух выражени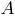й 
и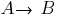 
выводит новое выражение 
.
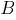В разной литературе можно встретить разные названия метода правил вывода, например, правила дедуктивных выводов или более часто modus ponens. Принцип работы правил вывода хорошо иллюстрирует следующий пример:
«Если известно, что высказывание «А» влечет (имплицирует) высказывание «В», а также известно, что высказывание «А» истинно, то, следовательно, «В» истинно»
В логике предикатов имеются универсальные правила, оперирующие с формулами, содержащими свободные переменные. Решение задач (получение выводов) в логических моделях может основываться на применении подобных правил к исходной совокупности истинных предикатов как доказательство правильности какого-либо составного предиката. Такой способ получения решения называется неаксиоматическим или другими словами – натуральным, естественным и совпадает со способами вывода в продукционных моделях.
Поскольку ответ получается как заключение из комбинации уже существующих логических формул, то по аналогии с выводами в продукционных моделях его можно назвать прямым (обратным) выводом. Однако всегда следует учитывать, что в формальной логике причинно-следственные отношения игнорируются.
Суть процедуры вывода заключается в рекурсивном применении подстановки известных значений в составной предикат. При этом принципиально гарантируется, что доказательство истинности результата можно проверить формальной процедурой.
Если в формальной логической модели механизм логического вывода использует метод правил вывода, то есть основания эту модель отнести к продукционным или логико-лингвистическим.
Пример: вывод решения в логической модели на основе правила вывода – modus ponens.
Даны утверждения:
- «Сократ – человек»;
- «Человек – это живое существо»;
- «Все живые существа смертны».
Требуется доказать утверждение «Сократ смертен».
Решение:
Шаг 1. Представим высказывания в предикатной форме:
Шаг 2. На основе правила вывода (modus ponens) и подстановки (Сократ/X) в первом предикате получим утверждение:
«Сократ – это живое существо»
Шаг 3. На основе правила вывода (modus ponens) и подстановки (Сократ/Y) в третьем предикате получим утверждение:
«Сократ – смертен»