В классическом генетическом алгоритме используется двоичное представление хромосом, селекция методом колеса рулетки и точечное скрещивание (с одной точкой скрещивания). Для повышения эффективности его работы создано множество модификаций основного алгоритма. Они связаны с применением других методов селекции, с модификацией генетических операторов (в первую очередь оператора скрещивания), с преобразованием функции приспособленности (путем ее масштабирования), а также с иными способами кодирования параметров задачи в форме хромосом. Существуют также версии генетических алгоритмов, позволяющие находить не только глобальный, но и локальные оптимумы. Это алгоритмы, использующие так называемые ниши, введенные в генетические алгоритмы по аналогии с природными экологическими нишами. Другие версии генетических алгоритмов служат для многокритериальной оптимизации, т.е. для одновременного поиска оптимального решения для нескольких функций. Встречаются также специальные версии генетического алгоритма, созданные для решения проблем малой размерности, не требующих ни больших популяций, ни длинных хромосом. Их называют генетическими микроалгоритмами.
Методы селекции
Стандартный метод селекции – рулетка – обладает рядом недостатков. Один из них следующий: особи с очень малым значением функции приспособленности слишком быстро исключаются из популяции, что может привести к преждевременной сходимости генетического алгоритма. Поэтому созданы и используются альтернативные алгоритмы селекции, например турнирная и ранговая селекции. При турнирной селекции все особи популяции разбиваются на подгруппы с последующим выбором в каждой из них особи с наилучшей приспособленностью. Подгруппы могут иметь произвольный размер, но чаще всего популяция разделяется на подгруппы по 2-3 особи в каждой. При ранговой селекции особи популяции ранжируются по значениям их функции приспособленности. Это можно представить себе как отсортированный список особей, упорядоченных по направлению от наиболее приспособленных к наименее приспособленным (или наоборот), в котором каждой особи приписывается число, определяющее ее место в списке и называемое рангом. Количество копий каждой особи, введенных в родительскую популяцию, рассчитывается по априорно заданной функции в зависимости от ранга особи.
Элитные методы отбора гарантируют, что при отборе обязательно будут выживать лучший или лучшие члены популяции совокупности. При этом часть самых лучших особей без каких-либо изменений переходит в следующее поколение.
Двухточечное скрещивание и равномерное скрещивание
В двухточечном кроссинговере (двухточечное скрещивание) выбираются две точки разрыва, и родительские хромосомы обмениваются участком генетического кода, который находится между двумя этими точками. В равномерном кроссинговере (равномерное скрещивание), каждый бит первого родителя наследуется первым потомком с заданной вероятностью; в противном случае этот бит передается второму потомку. И наоборот.
Размер популяции
Размер популяции является весьма важным элементом генетических алгоритмов. Если популяция слишком мала, генетического материала может не хватить для решения задачи. Размер популяции также влияет на коэффициент применения операторов скрещивания и мутации.
Методы кодирования
В классическом генетическом алгоритме применяется двоичное кодирование хромосом. Оно основано на известном способе записи десятичных чисел в двоичной системе, где каждый бит двоичного кода соответствует очередной степени цифры 2. Например, двоичная последовательность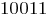 
представляет собой код числа 
:
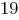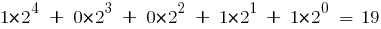
В генетических алгоритмах можно, например, использовать код Грея, который характеризуется тем, что двоичные последовательности, соответствующие двум последовательным целым числам, отличаются только одним битом. Такой способ кодирования хромосом может оказаться оправданным при использовании операции мутации.