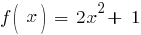Пример применения генетического алгоритма

Выбор исходной популяции для генетического алгоритма связан с представлением параметров задачи в форме хромосом, т.е. с так называемым хромосомным представлением. Это представление определяется способом кодирования. В классическом генетическом алгоритме применяется двоичное кодирование, т.е. аллели всех генов в хромосоме равны 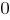или 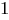. Длина хромосом зависит от условий задачи, точнее говоря – от количества точек в пространстве поиска.

Очень часто применение генетических алгоритмов сводится к решению задач оптимизации. Рассмотрим очень простой пример – задачу нахождения максимума функции:

Формула 1

для целочисленной переменной 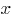$x$ , принимающей значения от 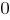до $31$ .

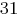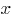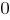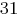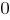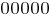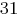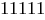Для применения генетического алгоритма необходимо, прежде всего, закодировать значения переменной $x$ в виде двоичных последовательностей. Очевидно, что целые числа из интервала от до $31$ можно представить последовательностями нулей и единиц, используя их представление в двоичной системе счисления. Число при этом записывается как $00000$ , а число $31$ – как $11111$ . В данном случае хромосомы приобретают вид двоичных последовательностей, состоящих из 5 битов, т.е. цепочками длиной 5.

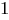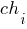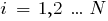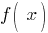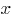Также очевидно, что в роли функции приспособленности будет выступать целевая функция, заданная формулой . Тогда приспособленность хромосомы $ch_{i}$ , $i~=~1,2~...~N$ будет определяться значением функции $f(~x)$ для $x$ , равного фенотипу, соответствующему генотипу 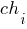$ch_{i}$ . Обозначим эти фенотипы 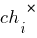${ch_{i}}^*$ . В таком случае значение функции приспособленности хромосомы 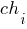$ch_{i}$ (т.е. 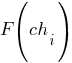$F(ch_{i})$ ) будет равно $f(~{ch_{i}}^*)$ .

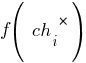Выберем случайным образом исходную популяцию, состоящую из 6 кодовых последовательностей (например, можно 30 раз подбросить монету); при этом 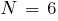$N~=~6$ . Допустим, что выбраны хромосомы:

$ch_{1}~=~10011$	$ch_{2}~=~00011$
$ch_{3}~=~00111$	$ch_{4}~=~10101$
$ch_{5}~=~01000$	$ch_{6}~=~11101$

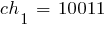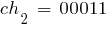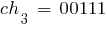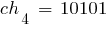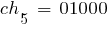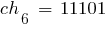Соответствующие им фенотипы – это представленные ниже числа:

${ch_{1}}^*~=~19$	${ch_{2}}^*~=~3$
${ch_{3}}^*~=~7$	${ch_{4}}^*~=~21$
${ch_{5}}^*~=~8$	${ch_{6}}^*~=~29$

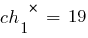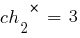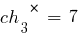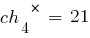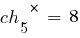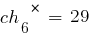По формуле рассчитываем значения функции приспособленности для каждой хромосомы в популяции:

$F(ch_{1})~=~723$	$F(ch_{2})~=~19$
$F(ch_{3})~=~99$	$F(ch_{4})~=~883$
$F(ch_{5})~=~129$	$F(ch_{6})~=~1683$

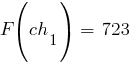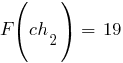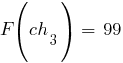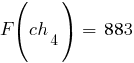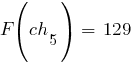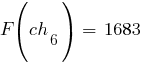Селекцию хромосом проводим методом рулетки. Для этого выбираем 6 хромосом для репродукции. Колесо рулетки представлено на рисунке.

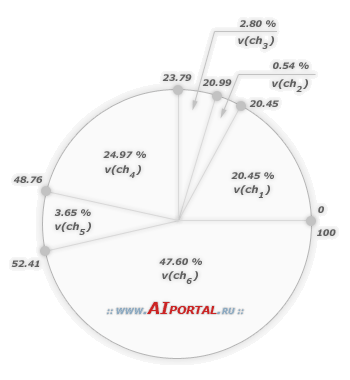
Допустим, что выбраны числа: 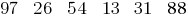$97~~26~~54~~13~~31~~88$

Это означает выбор хромосом: 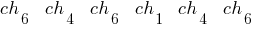$ch_{6}~~ch_{4}~~ch_{6}~~ch_{1}~~ch_{4}~~ch_{6}$

Пусть скрещивание выполняется с вероятностью 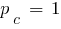$p_{c}~=~1$ . Допустим, что для скрещивания сформированы пары:

$(ch_{1}~-~ch_{4})~,~(ch_{4}~-~ch_{6})~,~(ch_{6}~-~ch_{6})$

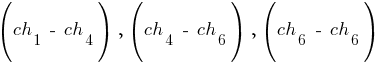
Кроме того, допустим, что случайным образом выбрана точка скрещивания, равная 3 для пары 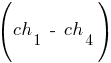$(ch_{1}~-~ch_{4})$ , а также точка скрещивания, равная 2 для пар $(ch_{4}~-~ch_{6})$ , $(ch_{6}~-~ch_{6})$ :

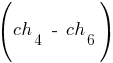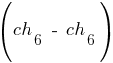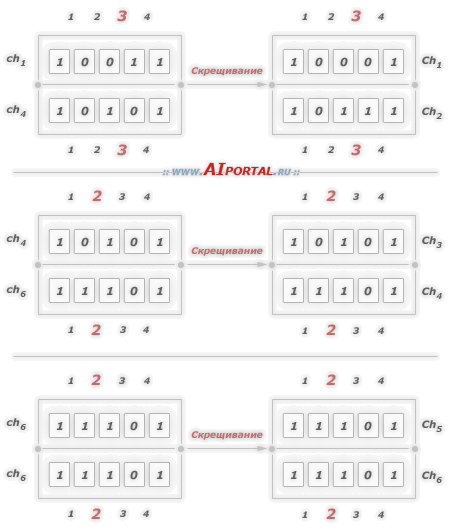
При условии, что вероятность мутации 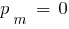$p_{m}~=~0$ , в новую популяцию включаются хромосомы:

$Ch_{1}~=~10001$	$Ch_{2}~=~10111$
$Ch_{3}~=~10101$	$Ch_{4}~=~11101$
$Ch_{5}~=~11101$	$Ch_{6}~=~11101$

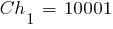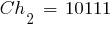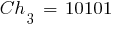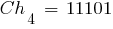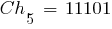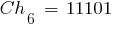Для расчета значений функции приспособленности этих хромосом необходимо декодировать представляющие их двоичные последовательности и получить соответствующие им фенотипы. Обозначим их 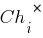${Ch_{i}}^*$ . В результате декодирования получаем:

${Ch_{1}}^*~=~17$	${Ch_{2}}^*~=~23$
${Ch_{1}}^*~=~21$	${Ch_{4}}^*~=~29$
${Ch_{5}}^*~=~29$	${Ch_{6}}^*~=~29$

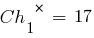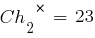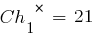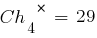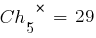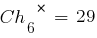Соответственно, значения функции приспособленности хромосом новой популяции, рассчитанные по формуле 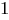, составят:

$F(Ch_{1})~=~579$	$F(Ch_{2})~=~1059$
$F(Ch_{3})~=~883$	$F(Ch_{4})~=~1683$
$F(Ch_{5})~=~1683$	$F(Ch_{6})~=~1683$

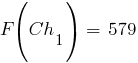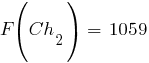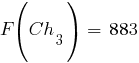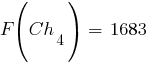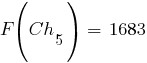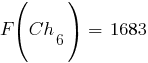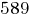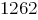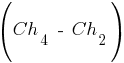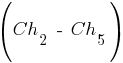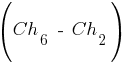Легко заметить, что в этом случае среднее значение приспособленности возросло с $589$ до $1262$ . Обратим внимание, что если на следующей итерации будут сформированы для скрещивания пары хромосом, например, $(Ch_{4}~-~ Ch_{2})$ , $(Ch_{2}~-~ Ch_{5})$ и $(Ch_{6}~-~ Ch_{2})$ с точкой скрещивания 2 или 3, то среди прочих будет получена хромосома 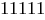$11111$ с фенотипом, равным числу 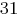$31$ , при котором оптимизируемая функция достигает своего максимума. Значение функции приспособленности для этой хромосомы оказывается наибольшим и составляет 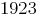$1923$ . Если такое сочетание пар в данной итерации не произойдет, то можно будет ожидать образования хромосомы с наибольшим значением функции приспособленности на следующих итерациях. Хромосома 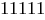$11111$ могла быть получена и на текущей итерации в случае формирования для скрещивания пары 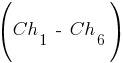$(Ch_{1}~-~ Ch_{6})$ с точкой скрещивания 3.

Следует упомянуть, что в малых популяциях часто встречаются ситуации, когда на начальном этапе несколько особей имеют значительно большие значения функции принадлежности, чем остальные особи данной популяции. Применение метода селекции на основе колеса рулетки позволяет в этом случае очень быстро выбрать «наилучшие» особи, иногда – на протяжении «жизни» одного поколения. Однако такое развитие событий считается нежелательным, поскольку оно становится главной причиной преждевременной сходимости генетического алгоритма, называемой сходимостью к неоптимальному решению. По этой причине используются и другие методы селекции, отличающиеся от колеса рулетки, либо применяется масштабирование функции приспособленности.

В заключении отметим, что при длине хромосом, равной 5 битам, пространство поиска очень мало и насчитывает всего 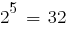$2^5~=~32$ точки. Представленный пример имеет исключительно демонстрационный характер. Применение генетического алгоритма для такого простого примера практически нецелесообразно, поскольку его оптимальное решение может быть получено мгновенно. Однако этот пример пригоден для изучения функционирования генетического алгоритма.