
Под классификацией понимается система группировки множества объектов, составленная на основе учета общих признаков этих объектов и закономерных связей между ними.
Целью классификации является образование групп схожих между собой объектов, которые принято называть классами или кластерами. Слово кластер английского происхождения (cluster), переводится как сгусток, пучок, группа. Родственные понятия, используемые в литературе, – таксон, сгущение, сегмент.
При геометрическом подходе в основе применения методов классификации лежит так называемая гипотеза компактности. Согласно ей, близким в содержательном смысле объектам в геометрическом пространстве признаков соответствуют обособленные множества точек, обладающие свойствами хорошей отделимости. А именно:
- множества разных образов соприкасаются в сравнительно небольшом числе точек, либо вообще не соприкасаются и разделены точками, не принадлежащими ни одному из классов;
- границы классов имеют сравнительно плавную форму – не изрезаны, и у классов отсутствуют глубокие выступы в пределы других классов.
В результате различные классы при выполнении гипотезы компактности могут быть разделены достаточно простыми гиперповерхностями.
Иллюстрация выполнения и невыполнения гипотезы компактности приведена на рисунке.
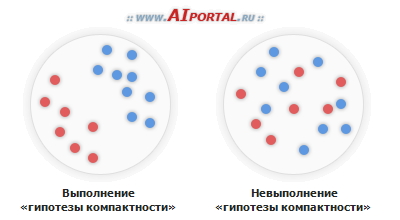
Гипотеза компактности дает на практике хорошие результаты классификации, если есть достаточное соответствие между содержанием выделенных признаков и построенным геометрическим пространством.
Обобщением гипотезы компактности является гипотеза простой геометрической структуры. Она заключается в следующем: сходным в содержательном смысле объектам классификации соответствует простая структура в геометрическом пространстве признаков: расположенность вдоль прямой, на окружности, в сфере, по спирали, на решетке и т.п. Во многих случаях, когда условия решаемой задачи задают определенную структуру объектов, применение данной гипотезы и соответствующих алгоритмов классификации приводят к хорошим практическим результатам и хорошо согласуются с представлениями человека о получаемых классах образов.
На основе гипотезы компактности разработано множество алгоритмов классификации. В рамках многомерных статистических методов для этой цели развиваются методы кластерного анализа.